0) First Things First
Welcome to the first lesson in the TinyDiffRast project! Before diving into the fun stuff, there are a few things to discuss.
Contents
Project Scope
We should start by clarifying the scope of this project. In this tiny course, we will be exploring the world of inverse rendering.
So, what is inverse rendering? We can think of regular forward rendering as a simulation of the process of photography or videography. In the real world, light is emmitted by various sources and bounces around a 3D environment interacting with different physical objects. We can take photographs and videos of the environment by capturing some of this light with a camera. Forward rendering algorithms simulate this process in virtual worlds with varying degrees of fidelity and computational efficiency. Inverse rendering algorithms aim to solve this simulation in reverse. Given a set of 2D images that were created by some process of light transport, inverse rendering seeks to deduce the properties of the 3D scene (e.g. lighting, geometry, material and camera properties) that gave rise to the images. Needless to say, the inverse problem is quite a bit harder than the forward problem, however, it is frequently a very useful problem to solve. Inverse rendering allows us to use information contained in 2D images to infer properties of 3D scenes.
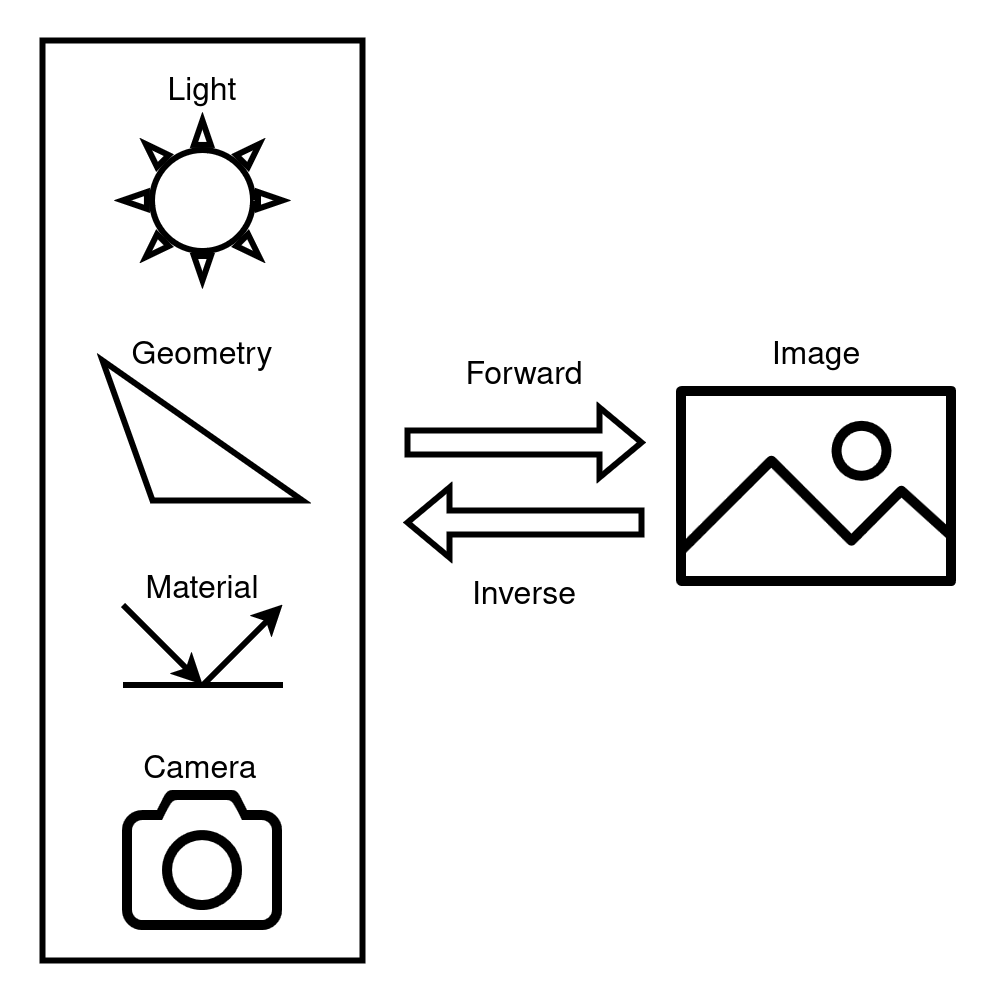
The approach that is typically taken to tackle the inverse rendering problem is called differentiable rendering. Let us denote the forward rendering process as a function \(f: x \rightarrow y\), where \(x\) represents the scene parameters and \(y\) the image data, and \(f^{-1}: y \rightarrow x\) as the inverse process. Unfortunately, even when provided with \(y\) and \(f\), computing \(f^{-1}\) and \(x\) is not at all straightforward. What we can often do, however, is compute the derivative \(\frac{\partial f}{\partial x}\). This derivative is useful because it allows us to gradually update scene parameters \(x\) so as to make the image data produced by \(f(x)\) gradually more similar to some ground truth image data. This process of learning scene parameters using derivatives is very similar to the process used to train neural networks. The same optimization algorithm (gradient descent) is often used. The key difference is that, in the differentiable rendering scenario, the function \(f\) is a light transport simulation and not a neural network.
This, however, still does not narrow the scope enough for us to get started, for there are many different approaches to differentiable rendering and we cannot cover them all at once. In this project, we will further constrain ourselves to a type of rendering called triangle rasterization. We think this is a good place to begin for several reasons. Triangle rasterization was one of the first rendering approaches developed, and it remains one of the most used approaches today. Furthermore, rasterization is one of the more computationally efficient rendering approaches. It must be said that rasterization does have it’s limitations. There are many optical effects that a rasterization approach is poorly suited to simulate (e.g. refraction and inter-reflections) and even relatively simple effects like shadows can be tricky to implement using rasterization. Nevertheless, there is a reason that rasterization has not yet been consigned to the past, and for our purposes, it will serve very well to introduce the fundamentals of differentiable rendering.
Therefore, the primary objective of this project will be to explore, explain and implement two different state-of-the-art inverse rendering approaches that rely on triangle rasterization: Nvdiffrast (NVDR) an approach proposed by Nvidia researchers in 2020, and Rasterize-Then-Splat (RTS) an approach proposed by Google researchers in 2021. In doing so, we will encounter and overcome some of the prinicpal challenges associated with differentiable rendering. These methods are found in several sofware packages for 3D machine learning: PyTorch3D, developed and maintained by Meta, Tensorflow Graphics developed and maintained by Google, and Kaolin developed and maintained by Nvidia. NVDR and RTS are not the only differentiable triangle rasterization approaches included in these packages, but they are some of the most recent and, as we will see later, they have several advantages over other approaches.
Development Environment
The second matter to resolve before getting started is selecting and setting up a development environment. In this project, we will not just be discussing differentiable rasterization approaches, but we will also be implementing them from scratch. The primary motivation for re-implementing these approaches is to provide clearer and more accesible educational material. The implementations provided by those packages are optimized for performance and not intelligibility. In general, it is not a simple matter to edit the implementations provided by existing software packages for the purposes of research and exploration
The algorithms provided by these packages are, for the most part, implemented using CUDA. For those who are not aware, CUDA is a toolkit developed by Nvidia to enable general computing on Nvidia GPUs. CUDA is an essential tool for developing high performance GPU accelerated programs and is used by many machine learning (ML) framworks. However, CUDA code is relatively low-level, can be quite difficult to read and write, and will only run on machines with a Nvidia GPU. Furthermore, CUDA does not support automatic differentiation. This means that if one wants to compute the derivative of a function (as we will), one must derive the function manually and implement a second function to compute the derivative. In addition to being time consuming, one must carefully test the gradient function to ensure that it was implemented correctly. If one then wishes to alter their original function, they must also update their derivative function to prevent the implementations from diverging. It is for these reasons that ML libraries like PyTorch, Tensorflow, and Jax were developed. Within these libraries, primitive operations can be combined to build complex functions whose derivatives can be computed without needing to manually derive or implement custom derivative functions. Such libraries have had a profound impact within the ML community and have lead to improvements in productivity and a reduction in the number of headaches due to incorrect custom derivative code.
So then, why not simply implement differentiable rasterization approaches in a ML framework? ML frameworks were designed for particular workloads, specifically those encountered in the field of deep learning. These workloads typically involve large tensor operations and relatively little algortithmic dynamism. For example, a deep convolutional neural network takes in a tensor and performs a series of computationally expensive tensor operations that are always the same regardless of the input tensor values. This algorithm is static (known at compile time) and most of the computational cost is associated with operations on large tensors. ML frameworks were designed to solve this class of problem, and they do so very well. Rendering algorithms, on the other hand, tend to have different characteristics. Most operations in rendering algorithms involve small data types with a great deal of algorithmic dynamism. For example, during triangle rasterization, many triangles are processed in parallel. How each triangle is processed depends on the values of the triangle vertices, which are not known at compile time. Therefore, a rasterization algorithm requires fine control flow within a parallel computing framework. This is not something that ML frameworks handle very well. You can sometimes use masks and other workarounds to get the job done, but this is inefficient and makes for complicated code. Aside from control flow, there are other aspects of rendering algorithms (such as non-tensorial data structures) that are not typically well supported by ML frameworks. Because of this, trying to implement rendering algorithms directly using a ML framework can cause even more headaches than writing custom derivative code.
Thankfully, compiler engineers and developers have recognized the need for new computing frameworks. Several alternative GPU computing frameworks have now been released that support automatic differentiation, and the types of data structures and control flow that are frequently required in rendering algorithms. Dr. Jit was developed specifically for the application of differentiable ray tracing. More recently, the shading language Slang announced first class support for automatic differentiation, targeting inverse rendering applications. I believe that there is much more to be written on this topic, and I’m sure that the next generation of computing frameworks will have profound impacts in ML, inverse rendering, and many other computational fields. If you are interested in diving deeper into this space, the SlangD paper Appendix C includes an excellent discussion of the design space of automatic differentiation frameworks. Additionally, Christopher Rackauckas has written a few good blog posts (1, 2) on the topic. For now, we will return to the task of selecting a framework for our project.
The programming framework that will be used within this course is Taichi. Here are the reasons why it was selected. Taichi is embedded within Python and is easy to read and write. Taichi supports both CUDA and CPU backends. This means that you can run Taichi code without needing to buy a Nvidia GPU (which are not exactly cheap these days). It also means that if you have a Nvidia GPU, the code will run fast. Speaking of Nvidia, the Warp framework is extremely similar to Taichi and may even be more advanced at the time of writing this. We chose Taichi because it has a more permissive license, but if you don’t mind the Warp terms of use, you could certainly use it for this course instead. Taichi supports automatic differentiation. This makes it much easier to try out new ideas without needing to write, test, and maintain custom code for derivatives. Taichi follows a single instruction multiple data (SIMD) programming model, similar to Slang. This is a good programming model for what we will be doing, and allows for intricate control flow in highly parallelized algorithms. If you are curious about SIMD programming models, the SlangD paper makes some compelling arguments for why it is the best choice in inverse rendering applications. Taichi has good support for advanced data structures. Taichi also has good support for real-time and interactive visualizations. We will be using this quite a lot in our demos. Like all good things, Taichi also has it’s shortcomings, but for the purposes of this project, we believe it is the best available choice. As you will soon see, using Taichi, we will be able to implement differentiable rasterization approaches, from scratch, in accessible, cross-platform, and surprisingly performant code. If some, or most, of this discussion didn’t make much sense to you, fear not! The relevant aspects of Taichi will be explained as we progress.
Prerequisites
A moderate level of mathematical and computational knowledge will be required to follow the material in the course. Overall, we believe that it should be accessible to anyone who has completed a quantitative undergraduate degree like engineering or computer science, is close to doing so, or has a comparable knowledge base. We will assume that you know how to program (classes, functions, loops, conditionals, etc…), that you know what a derivative and a gradient is, and that you know some linear algebra. Ideally, you would also know a little bit about rendering (we recommend the excellent tiny renderer course to begin). It will also help if you have some experience with automatic differentation and gradient-based optimzation. We will do our best to provide links to additional educational material whenever appropriate. If you are unsure if you have sufficient knowledge, just give it a shot! You can always study up on a topic if you find it necessary.
Coding Challenge 0
For those of you who wish to code along with us as we go, we will be including some programming challenges at the end of each blog lesson. Solutions to each challenge, typically a working implementation of some system component, will always be available in our codebase for you to review if you wish.
As is tradition, the first challenge will be to get a development environment set up with a working “Hello World!”. For this, you need simply follow the instructions provided in the Taichi docs. I also encourage you to check out some the examples provided in the Taichi gallery to get a sense of the cool things that you can do with Taichi.
Conclusion
In this lesson, we laid out the objectives of this project. We also selected the Taichi framework and set up a development environment. In the next lesson, we will dive into the world of differentiable rasterization and begin writing our own Taichi code.